Monroe on Embedding Right Continuous Martingales in Brownian Motion

The martingale representation theorem states that any martingale adapted with respect to a Brownian motion can be expressed as a stochastic integral with respect to the same Brownian motion.

Theorem 1 Let B be a standard Brownian motion defined on a probability space ${(\Omega,\mathcal{F},{\mathbb P})}$ and ${\{\mathcal{F}_t\}_{t\ge 0}}$ be its natural filtration.

Then, every ${\{\mathcal{F}_t\}}$ –local martingale M can be written as

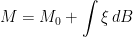
$\displaystyle M = M_0+\int\xi\,dB$

for a predictable, B-integrable, process ${\xi}$ .

As stochastic integration preserves the local martingale property for continuous processes, this result characterizes the space of all local martingales starting from 0 defined with respect to the filtration generated by a Brownian motion as being precisely the set of stochastic integrals with respect to that Brownian motion. Equivalently, Brownian motion has the predictable representation property. This result is often used in mathematical finance as the statement that the Black-Scholes model is complete. That is, any contingent claim can be exactly replicated by trading in the underlying stock. This does involve some rather large and somewhat unrealistic assumptions on the behaviour of financial markets and ability to trade continuously without incurring additional costs. However, in this post, I will be concerned only with the mathematical statement and proof of the representation theorem.

In more generality, the martingale representation theorem can be stated for a d-dimensional Brownian motion as follows.

Theorem 2 Let ${B=(B^1,\ldots,B^d)}$ be a d-dimensional Brownian motion defined on the filtered probability space ${(\Omega,\mathcal{F},\{\mathcal{F}_t\}_{t\ge 0},{\mathbb P})}$ , and suppose that ${\{\mathcal{F}_t\}}$ is the natural filtration generated by B and ${\mathcal{F}_0}$ .

$\displaystyle \mathcal{F}_t=\sigma\left(\{B_s\colon s\le t\}\cup\mathcal{F}_0\right)$

Then, every ${\{\mathcal{F}_t\}}$ -local martingale M can be expressed as

$\displaystyle M=M_0+\sum_{i=1}^d\int\xi^i\,dB^i$ (1)

for predictable processes ${\xi^i}$ satisfying ${\int_0^t(\xi^i_s)^2\,ds<\infty}$ , almost surely, for each ${t\ge0}$ .

As Brownian motion ${B^i}$ has quadratic variation ${[B^i]_t=t}$ , the condition that ${\int_0^t(\xi^i_s)^2\,ds}$ is finite is equivalent to stating that ${\xi^i}$ is Bⁱ-integrable. Taking the quadratic covariation of (1) with ${B^i}$ and using the identity ${[B^i,B^j]=0}$ for ${i\not=j}$ gives

$\displaystyle [M,B^i]=\int\xi^i_s\,ds.$

By Lebesgue's theorem, this shows that ${\xi^i_t}$ is given by the derivative

$\displaystyle \xi^i_t=\frac{d}{dt}[M,B^i]_t$

for almost every t.

Proving the representation theorem involves showing that, for all integrable random variables Z, there exist predictable and ${B^i}$ -integrable processes ${\xi^i}$ satisfying

$\displaystyle {\mathbb E}[Z\mid\mathcal{F}_t]={\mathbb E}[Z\mid\mathcal{F}_0]+\sum_i\int_0^t\xi^i\,dB^i$

(2)

(almost surely), for each time ${t}$ . As long as this can be shown to hold for a suitably large set of random variables, the representation theorem will follow.

I now give an argument showing that (2) is indeed satisfied for certain B-measurable random variables. Equation (2) can be verified directly for random variables of the form

$\displaystyle Z=U\exp\left(i\sum_j\int_0^\infty\alpha^j\,dB^j\right)$

(3)

for deterministic processes ${\alpha^j}$ satisfying ${\int_0^\infty(\alpha^j_t)^2\,dt<\infty}$ (for now, i denotes the square root of -1) and ${\mathcal{F}_0}$ -measurable variable U. In particular, for a sequence of times ${T_1,\ldots,T_n}$ and ${a_1,\ldots,a_n\in{\mathbb R}^d}$ , taking ${\alpha^j=\sum_k 1_{(0,T_k]}(a_k)_j}$ gives

$\displaystyle Z=U\exp(ia_1\cdot B_{T_1}+\cdots + ia_n\cdot B_{T_n}).$

As ${\int_t^\infty\alpha^j\,dB^j}$ are normal with zero mean and variance ${\int_t^\infty(\alpha^j_s)^2\,ds}$ independently of ${\mathcal{F}_t}$ , the expectation can be written out as

$\displaystyle {\mathbb E}\left[Z\mid\mathcal{F}_t\right]=U\exp\left(i\sum_j\int_0^t\alpha^j\,dB^j-\frac12\sum_j\int_t^\infty(\alpha^j_s)^2\,ds\right).$

This is continuous and, setting ${M_t={\mathbb E}[Z\mid\mathcal{F}_t]}$ , Ito's lemma gives

$\displaystyle M_t=M_0+i\sum_j\int_0^tM\alpha^j\,dB^j,$

so, taking ${\xi^j=iM\alpha^j}$ shows that (2) is satisfied for all random variables of the form (3).

Alternatively, it can be shown that (2) holds for all random variables of the form ${Z=F(B_T)}$ , for a bounded measurable function ${F\colon{\mathbb R}^d\rightarrow{\mathbb R}}$ and time T. For times ${t<T}$ , ${B_T-B_t}$ is, by definition, joint normal with covariance matrix ${(T-t)I}$ independently of ${\mathcal{F}_t}$ . This allows us to write out ${{\mathbb E}[Z_T\mid\mathcal{F}_t]}$ for all ${t<T}$ as a function of ${B_t}$ ,

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} &\displaystyle{\mathbb E}\left[F(B_T)\mid\mathcal{F}_t\right]=f(t,B_t),\smallskip\\ &\displaystyle f(t,x)=\frac1{\sqrt{2\pi(T-t)^d}}\int_{{\mathbb R}^d}e^{-\frac{(y-x)^2}{2(T-t)}}F(y)\,dy. \end{array}$

From this, it can be seen that f is twice continuously differentiable, so Ito's formula can be applied,

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} \displaystyle f(t,B_t) =&\displaystyle f(0,B_0)+\sum_i\int_0^t f_i(s,B_s)\,dB^i_s\smallskip\\ &\displaystyle + \int_0^t\left(f_t(s,B_s)+\frac12\sum_if_{ii}(s,B_s)\right)\,ds. \end{array}$

(4)

Here the subscripts t and i represent the partial derivatives of ${f(s,x)}$ with respect to time and ${x^i}$ respectively. The final term on the right-hand-side of (4) is a continuous FV process, all the other terms being local martingales. As continuous FV local martingales are constant, this allows us to break (4) up into the following two equations,

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{c} \displaystyle f_t+\frac12\sum_if_{ii}=0,\smallskip\\ \displaystyle{\mathbb E}[Z\mid\mathcal{F}_t]=f(t,B_t)={\mathbb E}[Z\mid\mathcal{F}_0]+\sum_i\int_0^tf_i(s,B_s)\,dB^i. \end{array}$

The first of these is the Kolmogorov backward equation, and the second shows that ${Z=F(X_T)}$ does indeed satisfy the representation property (2) with integrands ${\xi^i_s=f_i(s,B_s)}$ . It should be clear that this argument is quite general, and applies to any continuous martingale which is Markov with twice continuously differentiable transition densities. In fact, it is not difficult to extend the argument to variables of the form

$\displaystyle Z=F(U,B_{T_1},B_{T_2},\ldots,B_{T_n})$

for times ${0\le T_1\le\cdots\le T_n}$ , ${\mathcal{F}_0}$ -measurable variable U and bounded measurable function ${F\colon{\mathbb R}^{1+nd}\rightarrow{\mathbb R}}$ . However, I will not do this here, as Z of the form (3) is already enough to prove the martingale representation theorem for Brownian motion.

From here, it is possible to extend (2) to all bounded measurable random variables, by taking limits and applying the monotone class theorem. Ito's isometry can be used to show that ${L^2}$ -convergence of the random variables implies convergence of the integrands ${\xi^i}$ . However, in the proof given here, I will instead make use of the following more general result, applying to all continuous local martingales. Given a continuous local martingale N, every other local martingale can be expressed as an integral with respect to N plus an `orthogonal' term. This is a useful result in its own right. In finance, it has applications to models of incomplete markets in which it is not possible to exactly replicate all contingent claims by trading in the underlying stock. Instead, it is only possible to replicate them up to an orthogonal (i.e., unhedgeable) term.

Lemma 3 Let N be a continuous local martingale and M be any other local martingale. Then, there exists an N-integrable process ${\xi}$ and local martingale L such that

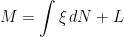
$\displaystyle M=\int\xi\,dN + L$

and [L,N]=0.

Proof: The lemma reduces to the statement that there is an N-integrable process ${\xi}$ satisfying ${[M,N]=\int\xi\,d[N]}$ . Then, defining ${L=M-\int\xi\,dN}$ gives

$\displaystyle [L,N]=[M,N]-\int\xi\,d[N]=0$

as required.

First, the FV process [M,N] is absolutely continuous with respect to [N]. That is, if ${\alpha}$ is a bounded process satisfying ${\int\alpha\,d[N]=0}$ , then ${\int\alpha\,d[M,N]=0}$ (almost surely). This follows from the Kunita-Watanabe inequality,

$\displaystyle \left\vert\int\alpha\,d[M,N]\right\vert\le\sqrt{[M]\int\alpha^2\,d[N]}.$

This implies that there exists a predictable process ${\xi}$ with ${[M,N]=\int\xi\,d[N]}$ . It needs to be shown that ${\xi}$ is N-integrable. That is, ${\int_0^t\xi^2\,d[N]}$ is almost-surely finite for each time t. This is, again, a consequence of the Kunita-Watanabe inequality. For any constant K,

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} \displaystyle\int1_{\{\vert\xi\vert<K\}}\xi^2\,d[N]&\displaystyle=\int1_{\{\vert\xi\vert<K\}}\xi\,d[M,N] \smallskip_underscore\&\displaystyle\le\sqrt{[M]\int1_{\{\vert\xi\vert<K\}}\xi^2\,d[N]}. \end{array}$

Cancelling the ${\int1_{\{\vert\xi\vert<K\}}\xi^2\,d[N]}$ term from the right hand side, squaring, and taking the limit ${K\rightarrow\infty}$ gives

$\displaystyle \int\xi^2\,d[N]\le[M]$

which is finite, as required. ⬜

This has the following d-dimensional generalization.

Lemma 4 Let ${N^1,N^2,\ldots,N^d}$ be continuous local martingales with covariations ${[N^i,N^j]=0}$ for ${i\not=j}$ . Then, every local martingale M can be expressed as

$\displaystyle M=\sum_{i=1}^d\int\xi^i\,dN^i+L$

for ${N^i}$ -integrable processes ${\xi^i}$ and local martingale L satisfying ${[L,N^i]=0}$ .

Proof: By Lemma 3, there are ${N^i}$ -integrable processes ${\xi^i}$ such that ${L^i\equiv N-\int\xi^i\,dN^i}$ satisfy ${[L^i,N^i]=0}$ . Setting ${L=M-\sum_i\int\xi^i\,dN^i}$ and using the condition that ${[N^j,N^i]=0}$ for ${i\not=j}$ gives

$\displaystyle [L,N^i]=[L^i,N^i]-\sum_{j\not=i}\int\xi^j\,d[N^j,N^i]=0.$

⬜

The martingale representation theorem follows immediately from applying the following to Lemma 4, so that the orthogonal term L is constant.

Lemma 5 Let ${B=(B^1,\ldots,B^d)}$ be a d-dimensional Brownian motion defined on the filtered probability space ${(\Omega,\mathcal{F},\{\mathcal{F}_t\}_{t\ge 0},{\mathbb P})}$ , and suppose that ${\{\mathcal{F}_t\}}$ is the natural filtration generated by B and ${\mathcal{F}_0}$ .

Then, any local martingale L satisfying ${[L,B^i]=0}$ for each i is constant.

Proof: By localization, it is enough to consider the case where L is a cadlag martingale and, replacing L by ${L-L_0}$ if necessary, we can assume that ${L_0=0}$ . Consider a bounded random variable Z satisfying (2). Then, ${M=\sum_i\xi^i\,dB^i}$ is a bounded martingale with covariation ${[L,M]=\sum_i\int\xi^i\,d[L,B^i]=0}$ . So, LM is a local martingale. As M is bounded and L is a martingale, LM will be of class (DL), so is a proper martingale. Then,

$\displaystyle {\mathbb E}[L_tZ]={\mathbb E}[L_tM_t]={\mathbb E}[L_0M_0]=0.$

For any fixed time t, consider the set S of bounded random variables Z satisfying ${{\mathbb E}[L_tZ]=0}$ . As shown above, this includes all Z of the form (3), which generate the sigma-algebra given by B. Also, dominated convergence implies that S is closed under taking limits of uniformly bounded sequences of variables. So, by the monotone class theorem, S contains all bounded random variables measurable with respect to ${\mathcal{F}_0}$ and B. In particular, if the filtration is generated by ${\mathcal{F}_0}$ and B then ${Z={\rm sgn}(L_t)}$ is in S, giving,

$\displaystyle {\mathbb E}[\vert L_t\vert]={\mathbb E}[L_tZ]=0,$

and ${L_t=0}$ (almost surely), as required. ⬜

kelleyrattind.blogspot.com

Source: https://almostsuremath.com/2010/05/25/the-martingale-representation-theorem/

Monroe on Embedding Right Continuous Martingales in Brownian Motion

0 Response to "Monroe on Embedding Right Continuous Martingales in Brownian Motion"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel

Monroe on Embedding Right Continuous Martingales in Brownian Motion

Related Posts

0 Response to "Monroe on Embedding Right Continuous Martingales in Brownian Motion"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel